통계-13 결측치

1. 결측치

결측치는 대부분의 시계열 데이터가 가지고 있는 문제이며 데이터가 누락되어 있는 것이다. 결측치가 있는 데이터로 분석을 진행하면 정확도와 신뢰도가 떨어질 수 있기 때문에 결측치를 전처리 하는 것은 필수적이다.

data = pd.DataFrame({
    'a':[1,2,np.nan,4,5],
    'b':[6,np.nan,8,9,10],
    'c':[11,12,13,np.nan,15]
})

print(data.isnull())

       a      b      c
0  False  False  False
1  False   True  False
2   True  False  False
3  False  False   True
4  False  False  False

결측치가 있는 데이터를 생성하고 innull 함수를 통해 어떤 부분이 결측치가 있는지 확인한다.

plt.figure(figsize=(8,6))
sns.heatmap(data.isnull(), cmap='viridis',cbar=False)

결측치가 있는 부분을 그래프로 시각화할 수 있다.

missing_count = data.isnull().sum()
print(missing_count)

a    1
b    1
c    1

sum 함수를 이용하여 각 행의 결측치 개수를 확인할 수 있다.

2. 결측치 삭제

np.random.seed(42)
dates = pd.date_range(start='2023-01-01', periods=100, freq='d')
values = np.random.randn(100)
values[10] = np.nan

data = pd.DataFrame({'date':dates,'value':values})

n10 = data.iloc[10]
print(n10)

date     2023-01-11 00:00:00
value                    NaN
Name: 10, dtype: object

100개의 날짜 데이터를 생성하고 10번을 결측치로 설정한다. iloc함수를 사용하여 10번이 결측치인 것을 확인할 수 있다.

data_without_missing = data.dropna(axis=0)
print(data_without_missing)

         date     value
0  2023-01-01  0.496714
1  2023-01-02 -0.138264
2  2023-01-03  0.647689
3  2023-01-04  1.523030
4  2023-01-05 -0.234153
..        ...       ...
95 2023-04-06 -1.463515
96 2023-04-07  0.296120
97 2023-04-08  0.261055
98 2023-04-09  0.005113
99 2023-04-10 -0.234587

[99 rows x 2 columns]

dropna 함수를 axis=0으로 설정하여 결측치가 있는 행을 모두 제거한다. 100개의 행에서 99개의 행으로 줄은 것을 알 수 있다.

 

결측치를 삭제하면 간단한 방법으로 삭제할 수 있고 시간적 흐름을 유지할 수 있지만 결국은 데이터 손실이 발생하며 결측치가 많은 경우 데이터의 크기가 크게 축소될 수 있고 해당 시점의 데이터를 알 수 없다.

따라서 결측치가 적거나 결측치가 특정구간에 몰려있는 경우, 시간의 연속성이 중요한 경우에 결측치 삭제를 고려할 수 있다.

3. 선형 보간

선형 보간은 데이터가 선형적인 특성을 가질 때 고려할 수 있으며 결측치 앞 뒤의 점을 직선으로 연결한다.

dates = pd.date_range(start='2023-01-01', periods=10, freq='d')
values = [1, np.nan,3,np.nan,5,6,np.nan,8,9,np.nan]

data = pd.DataFrame({'date':dates,'value':values})

결측치가 있는 데이터를 생성한다.

data['value_linear']=data['value'].interpolate(method='linear')
print(data)

        date  value  value_linear
0 2023-01-01    1.0           1.0
1 2023-01-02    NaN           2.0
2 2023-01-03    3.0           3.0
3 2023-01-04    NaN           4.0
4 2023-01-05    5.0           5.0
5 2023-01-06    6.0           6.0
6 2023-01-07    NaN           7.0
7 2023-01-08    8.0           8.0
8 2023-01-09    9.0           9.0
9 2023-01-10    NaN           9.0

interpolate의 linear 메소드를 사용하여 선형적인 보간 값을 생성하고 확인한다.

plt.plot(data['date'], data['value'],'o-', label = 'original')
plt.plot(data['date'], data['value_linear'],'x-', label = 'linear interpolation')
plt.xlabel('date')
plt.ylabel('value')
plt.title('linear interpolation')
plt.legend()
plt.show()

오리지널 데이터와 선형 보간한 데이터를 같이 그려서 확인해보면 결측치를 선형적으로 채운 것을 확인할 수 있다.

4. 스플라인 보간

스플라인 보간은 다항식을 이용하여 결측치를 부드러운 곡선으로 채우는 것이다. 결측치를 자연스럽게 이을 수 있지만 계산량이 많아진다.

np.random.seed(42)
dates = pd.date_range(start='2023-01-01', periods=100, freq='d')
values = np.random.randn(100)

data = pd.DataFrame({'date':dates,'value':values})

data.loc[10:20,'value'] = np.nan

100개의 데이터를 생성하고 10번~20번 구간을 결측치로 설정한다.

data['value_filled'] = data['value'].interpolate(method='linear')

스플라인 보간 법은 null 값에 사용할 수 없기 때문에 선형 보간을 먼저 실시한다.

from scipy.interpolate import CubicSpline

spl = CubicSpline(data.index, data['value_filled'])
data['value_spline'] = spl(data.index)

cubicspline 함수를 실행하여 스플라인 보간 값을 얻는다.

plt.plot(data['date'], data['value'],'o-', label = 'original')
plt.plot(data['date'], data['value_spline'],'x-', label = 'spline')
plt.xlabel('date')
plt.ylabel('value')
plt.title('spline')
plt.legend()
plt.show()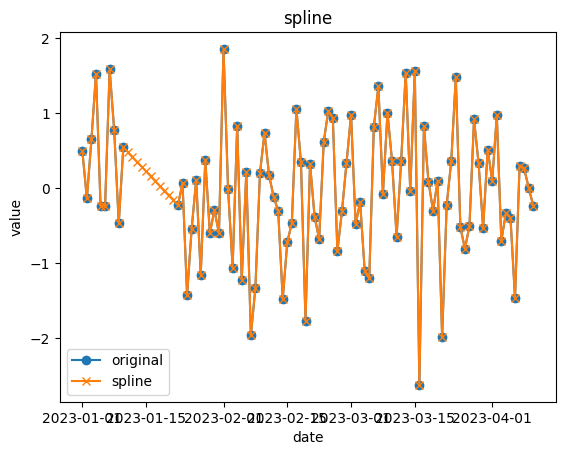

결측치를 스플라인 보간한 모습을 확인할 수 있다.

5. 최근접 이웃 보간

최근접 이웃 보간은 결측치를 가장 가까운 점의 값으로 대체하는 것이다. 간단하게 나타낼 수 있지만 선이 이산적인 형태로 나타나기 때문에 이산적 데이터에서 고려된다.

data['value_filled'] = data['value'].interpolate(method='nearest')
print(data.loc[10:20])

plt.plot(data['date'], data['value'],'o-', label = 'original')
plt.plot(data['date'], data['value_filled'],'x-', label = 'nearest')
plt.xlabel('date')
plt.ylabel('value')
plt.title('nearest')
plt.legend()
plt.show()

nearest 인자를 사용하여 최근접 보간을 적용하고 그래프로 결과를 확인한다.

6. 평균값 대체

평균값 대체는 결측치를 변수의 평균값으로 대체하는 것이다. 평균값 대처는 간단하고 평균값이 중심 경향을 나타내기 때문에 대체된 값은 변수의 중심 부분에 위치하지만 데이터의 평균값을 사용하기 때문에 전체 데이터의 표본 편차를 줄인다.

mean_value = data['value'].mean()
data['value_filled'] = data['value'].fillna(mean_value)

plt.plot(data['date'], data['value'],'o-', label = 'original')
plt.plot(data['date'], data['value_filled'],'x-', label = 'mean')
plt.xlabel('date')
plt.ylabel('value')
plt.title('mean')
plt.legend()
plt.show()

mean 함수로 데이터의 평균값을 계산하고 그래프로 확인한다.

7. 결측치 처리 이후 평가, 고려사항, 목적

1. 결측치 비율 확인

결측치의 처리 전후의 비율을 비교하여 결측치 비율이 낮아졌는지 확인한다.

2. 기술 통계량 비교

결측치 처리 전후의 기술 통계량을 비교하여 크게 변하지 않았는지 확인한다.

3. 시각화

결측치 처리 이후 시각화를 통해 데이터를 비교한다.

4. 예측 성능 평가

결측치 처리 이후 해당 모델을 실제로 사용하여 성능이 향상되었는지 확인한다.

 

결측치를 처리할 때는 결측치가 어떻게 분포되었는지, 어떤 패턴을 가지고 있는지 파악해야 하며 해당 결측치를 처리할 때 원본 데이터의 특성을 잘 유지하는 대체 방법을 사용해야 한다.

 

따라서 결측치 처리의 목적은 데이터의 완성도를 높이고 예측모델의 성능을 향상하며 데이터의 편향을 방지하는 것에 있다.