통계-8 확률 분포

1. 확률 분포

확률 분포란 확률가 특정한 값을 가질 확률을 나타내는 함수이다. 확률 분포는 확률 변수가 가진 값이 독립적인지 연속적인지에 따라 이산 확률 분포와 연속 확률 분포로 나뉜다. 이산 확률 분포에는 포아송, 베르누이, 이항, 기하 등의 분포가 해당되며 연속 확률 분포에는 정규, 카이제곱, 감마 등의 분포가 해당된다.

 

2. 누적분포함수, 확률질량함수, 확률밀도함수

누적분포함수란 주어진 확률 변수가 특정 값보다 작거나 같을 확률을 나타내는 함수이다. 누적의 의미는 특정 값보다 작은 값들의 확률을 누적해서 구한다는 의미이다.

확률질량함수란 주어진 이산 변수의 분포를 나타내는 함수이며 확률밀도함수는 주어진 연속 변수의 분포를 나타내는 함수이다.

 

3. 정규분포

정규분포는 대칭적인 종 모양의 분포이며 대부분의 자연 현상에서 나타나는 분포이다.

평균이 0이고 표준편차가 1인 정규분포를 표준정규분포라고 부른다. 이 표준정규분포를 따르게 하기 위하여 변환하는 과정이 표준화이다.

표준화는 데이터에서 평균을 빼고 표준편차로 나누며 데이터가 평균을 기준으로 얼마나 떨어져 있는지를 확인할 수 있다.

np.random.seed(42)
height = np.random.normal(loc=170,scale=10,size=100)
weight = np.random.normal(loc=70,scale=5,size=100)
data = pd.DataFrame({'Height':height,'Weight':weight})
data.to_csv('../data/human_data.csv',index=False)

사람 100명의 키와 몸무게를 랜덤하게 정규분포로 데이터프레임을 만들어 csv로 저장한다. 

data = pd.read_csv('../data/human_data.csv')

height = data['Height']
weight = data['Weight']

plt.hist(height, bins =10,alpha=0.5,label='height')
plt.hist(weight, bins =10,alpha=0.5,label='weight')
plt.legend(loc='upper right')
plt.show()

생성한 csv파일을 시각화한다.

height_mean, height_std = norm.fit(height)
height_x = np.linspace(height.min(),height.max(),100)
height_y = norm.pdf(height_x, height_mean,height_std)

weight_mean, weight_std = norm.fit(weight)
weight_x = np.linspace(weight.min(),weight.max(),100)
weight_y = norm.pdf(weight_x, weight_mean,weight_std)

plt.hist(height,bins=10,density=True,alpha=0.5,label='height')
plt.plot(height_x,height_y,label='height distribution')
plt.hist(weight,bins=10,density=True,alpha=0.5,label='weight')
plt.plot(weight_x,weight_y,label='weight distribution')
plt.legend(loc='upper right')
plt.show()

norm 함수는 정규분포를 위한 함수이고 fit함수는 모수추정함수이며 height와 weight를 넣어 키와 몸무게의 평균과 표준편차를 구한다. x축은 linespace 함수로 값의 범위를 설정해 주고 y축은 pdf함수로 확률밀도함수를 그려준다.

ensity를 true로 하면 값들을 확률밀도로 나타내기 위해 정규화를 할 수 있으며 면적이 1이 된다. plot으로 선그래프를 그려준다.

 

4. 이항분포

이항분포는 연속된 n번의 독립적인 시행에서 각 시행에서 확률 변수가 특정한 값을 가질 확률이다. n을 한번만 실행하여 결론에 도달하는 것은 베르누이 분포이다.

n=10
p=0.5
num_simulations =100
successes = np.random.binomial(n,p,num_simulations)

plt.hist(successes, bins=11, range=(0,10),alpha=0.5)
plt.xlabel('successes')
plt.ylabel('frequency')
plt.title('binomial distribution simulation')
plt.show()

시행 횟수를 10으로 성공확률을 0.5로 설정한다. binomical 함수로 시뮬레이션을 진행하여 시각화한다.

성공 횟수에 따른 빈도수를 확인할 수 있다. 성공확률을 0.5로 설정하였기 때문에 정규분포의 형태를 가진다.

 

5. 포아송 분포

포아송 분포는 일정 시간, 공간에서 독립적인 확률변수가 가지는 분포이다. 

lambda_param=3
num_simulations = 1000
events = np.random.poisson(lambda_param, num_simulations)

plt.hist(events, bins=10,alpha=0.5)
plt.xlabel('number of events')
plt.ylabel('frequency')
plt.title('poisson distribution simulation')
plt.show()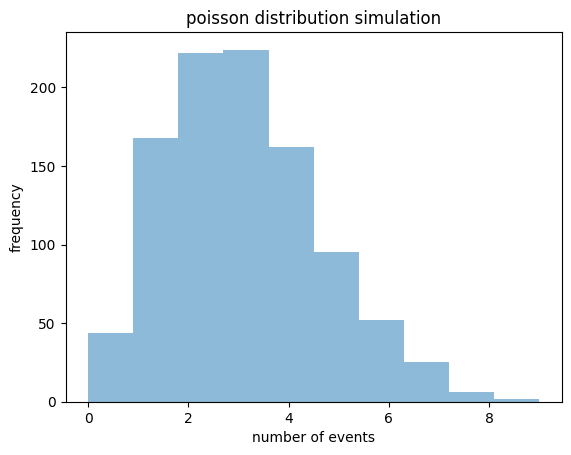

평균적인 사건 발생 횟수를 3으로 설정하고 poisson 함수를 시작하여 그래프로 나타낸다. 사건 발생 횟수에 따른 빈도를 확인할 수 있다. 

 

6. 지수 분포

지수분포는 지수 분포는 사건이 발생하고 또 같은 사건이 발생할 때까지 시간에 대한 확률 분포이다. 지수분포는 무기억성 특성을 가져서 과거의 사건이 미래의 사건에 영향을 미치지 않는다.

def generate_wating_time(lam,size):
    return np.random.exponential(scale=1/lam,size=size)

def measure_waiting_time(lam, num_samples):
    waiting_times = generate_wating_time(lam, num_samples)
    
    plt.hist(waiting_times, bins=30, density=True,alpha=0.7)
    plt.xlabel('waiting time')
    plt.ylabel('probablity density')
    plt.title('customer service center waiting time distribution')
    plt.show()
    
lam = 0.5
num_samples=1000
measure_waiting_time(lam,num_samples)

generate_waiting_time 함수는 exponential 함수를 사용하여 대기시간 샘플을 랜덤하게 생성한다. lam값과 size를 입력으로 받는데 lam값은 매개변수이며 평균 대기 시간의 역수이다. lam값이 클수록 대기 시간이 짧아지며 작을수록 대기시간이 길어진다. size는 생성할 샘플의 개수이다.

 

generate_waiting_time 함수를 measure_waiting_time 함수에 집어넣는다. 대기시간분포를 시각화하기 위하여 히스토그램을 그리고 lam값과 num_samples를 size로 전달한다.

 

마지막으로 0.5의 lam 값과 1000개의 샘플을 생성하여 함수를 돌려서 시각화한다. 그래프를 확인하면 대기 시간이 0~4에서 대부분 분포하고 있으며 대기시간이 길어질수록 발생확률이 감소한다.

 

7. 감마분포

감마분포는 평균 소요시간이 beta인 사건이 alpha번째 일어날 때까지 걸리는 시간에 대한 분포이다. 감마분포에는 alpha와 beta 두 가지 모수가 존재하며 형상모수와 척도모수라고 부른다. 감마분포에서 알파가 1이면 지수분포이다.

def generate_lifetime(alpha, beta, size):
    return np.random.gamma(shape=alpha,scale=beta, size=size)

def measure_lifetime(alpha, beta, num_samples):
    lifetime = generate_lifetime(alpha, beta, num_samples)
    plt.hist(lifetime, bins=30, density=True,alpha=0.7)
    plt.xlabel('life time')
    plt.ylabel('probablity density')
    plt.title('product lifetime distribution')
    plt.show()   
    
alpha = 2.5
beta = 1.2

num_samples= 1000
measure_lifetime(alpha, beta, num_samples)

alpha가 클수록 그래프를 좌측으로 왜곡되며 작을수록 우측으로 왜곡된다. beta가 클수록 분포의 높이는 낮아지고 폭이 좁아지며 작을수록 높이가 높아지고 폭이 넓어진다.

 

lifetime이 1.2인 제품이 2.5번째 고장까지의 분포를 확인할 수 있다.

 

8. 베타분포

베타분포는 0과 1사이의 값을 가지면 이항 분포에서 성공의 횟수가 확률 변수라면 베타분포에서는 성공의 비율이 확률 변수이다. alpha와 beta 두 개의 모수를 가지는데 각각 성공 횟수와 실패 횟수를 의미한다.

from scipy.stats import beta
alpha = 2
beta = 5

user_data = np.random.beta(alpha, beta, size=1000)

plt.hist(user_data, bins=30, density=True,alpha=0.7)
plt.xlabel('user behavior')
plt.ylabel('probablity density')
plt.title('user behavior distribution(alpha={}, beta={})'.format(alpha,beta))
plt.show()

0과 1사이의 데이터를 1000개를 생성한 후 beta함수를 돌린다. alpha는 2, beta는 5로 설정한다.

그래프를 확인해보면 x축은 데이터 분포, y축은 빈도수를 확인할 수 있으며 alpha 값이 높아질수록 성공확률이 증가하므로 그래프가 우측으로 이동하며 beta 값이 높으면 그래프가 좌측으로 이동한다.

9. 카이제곱 분포

카이제곱 분포는 감마 분포에서 alpha= p/2, beta = 2이고 p는 자유도이며 자유도는 합산하는 정규분포의 개수이다. 정규분포의 확률분포를 제곱하여 합산하였기 때문에 항상 양수의 값을 가진다.

from scipy.stats import chi2

df=5

random_variable = np.random.chisquare(df, size = 1000)

plt.hist(random_variable, bins=30, density=True,alpha=0.7)
plt.xlabel('random variable')
plt.ylabel('probablity density')
plt.title('chi_squared distribution(df={})'.format(df))
plt.show()

자유도가 5인 카이제곱 분포를 그래프로 그린다. 자유도가 증가할수록 넓어진다..

10. t분포

t분포는 정규분포보다 한단계 예측범위가 넓은 분포이다. 자유도가 커질수록 정규 분포에 가까워진다. 일반적으로 두 그룹 간의 평균차이를 비교하거나 회귀분석에서 독립 변수와 종속 변수의 관계를 분석할 때 사용한다.

from scipy.stats import t

df=10

random_simulations = 1000
t_values = np.random.standard_t(df, num_simulations)

plt.hist(t_values, bins=20,alpha=0.5)
plt.xlabel('t value')
plt.ylabel('frequency')
plt.title('t distribution simulation')
plt.show()

자유도를 10으로 설정하고 t검정 함수를 돌려 결과를 확인한다. t분포는 0을 중심으로 대칭이며 t값이 어떤 범위에서 어떤 빈도수를 가지고 있는지 확인한다.

11. f분포

 f분포는 두 개 이상의 그룹의 분산이 비교에 사용한다. 두개의 자유도를 가지고 있으며 df1, 분자의 자유도는 분산 비교에 참여한 그룹 수이고 df2, 분모의 자유도는 분산을 계산하는 표본의 수에서 분자의 자유도를 뺀 값이다. f분포는 비대칭 적이며 항상 양의 값을 가진다.

from scipy.stats import f

dfn = 5
dfd=10

num_simulations = 1000
f_values = np.random.f(dfn,dfd, num_simulations)

plt.hist(f_values, bins=20,alpha=0.5)
plt.xlabel('f value')
plt.ylabel('frequency')
plt.title('f distribution simulation')
plt.show()

자유도 1을 5, 자유도 2를 10으로 설정하여 f 모델 함수를 실행한다. 5개의 그룹을 비교하며 표본의 개수는 15개인 것을 알 수 있다. 이후에 f값에 대한 빈도수를 확인할 수 있고 오른 쪽으로 갈수록 평평해지는 것을 알 수 있다.