통계-16 ar, ma, arma, arima, sarima

1. 자기 회귀 모델(ar)

ar(autogressive)는 자기 자신을 종속 변수로 과거를 독립변수로 가지는 모델이다. 모델의 현재 값이 이전 값들의 선형조합으로 구성된다는 것을 의미한다.

np.random.seed(0)
n = 100
ar_params = [0.7]
ma_params = []
residuals = np.random.normal(0,1,n)

data = [0]
for i in range(1,n):
    data.append(ar_params[0] * data[i-1] + residuals[i])
    
df = pd.DataFrame({'date': pd.date_range(start= '2023-01-01',periods =n, freq='d'),'value': data})
df = df.set_index('date')
    
print(df.head())

               value
date                
2023-01-01  0.000000
2023-01-02  0.400157
2023-01-03  1.258848
2023-01-04  3.122087
2023-01-05  4.053019

ar계수를 0.7으로 설정하고 ma계수는 설정하지 않는다. 평균이 0이고 표준편차가 1인 잔차를 100개 생성한다. 초기값을 0으로 설정하고 이전시점의 데이터에 자기 회귀계수를 곱한 값에 현재 시점의 잔차를 더해서 다음 시점의 데이터를 계산하는 것을 반복한다.

from statsmodels.tsa.ar_model import AutoReg
from statsmodels.graphics.tsaplots import plot_acf

model = AutoReg(df['value'], lags=1)
result = model.fit()

print(result.summary())

plot_acf(df['value'],lags=20)

                            AutoReg Model Results                             
==============================================================================
Dep. Variable:                  value   No. Observations:                  100
Model:                     AutoReg(1)   Log Likelihood                -139.573
Method:               Conditional MLE   S.D. of innovations              0.991
Date:                Sun, 04 Jun 2023   AIC                            285.147
Time:                        13:11:05   BIC                            292.932
Sample:                    01-02-2023   HQIC                           288.297
                         - 04-10-2023                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0363      0.100      0.364      0.716      -0.159       0.232
value.L1       0.7776      0.064     12.115      0.000       0.652       0.903
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            1.2860           +0.0000j            1.2860            0.0000

autoreg 함수를 사용하여 모델을 생성한다. lags=1은 1차 자귀회귀모델을 의미한다. 모델을 학습시키고 summary로 모델의 정보를 확인한다. plot_acf로 자기상관 그래프를 출력하고 lags=20으로 시차의 개수를 20개로 지정한다.

 

summary를 확인해보면 const(상수항) 회구 계수가 0.0363이고 p-value가 0.716으로 유의미하지 않다는 것을 의미한다. lag1에 대한 회귀계수 value.l1은 0.7776, p-value가 0으로 유의미한 값을 가진다.

이 모델은 이전 시점의 값이 현재 시점에 유의미한 영향을 가진다는 것을 알 수 있다.

 

std err은 표준 오차를 의미하며 작을수록 신뢰성이 높다. z는 z-score를 의미하며 계수 추정치를 표준오차로 나눈 값이며 클수록 유의미하다. [0.025 0.975]는 추정된 계수의 신뢰 구간을 의미한다. 

 

ar.1의 real은 자기회귀 모델의 첫 번째 계수의 값을 의미한다. 자기 회귀 계수가 1에 가까울수록 현재시점의 데이터와 이전시점의 데이터가 선형적으로 관계가 있다는 것을 의미하며 1보다 크면 양의 상관관계를 1보다 작으면 음의 상관관계를 가지고 있다는 것을 의미한다. imaginary는 허수를 나타내며 modulus는 복소수의 크기를 나타내고  ferquency는 복소수의 주파수를 나타낸다. 계수는 1.2860이며 실수만 존재한다는 것을 알 수 있다.

 

x축은 시차이고 y축은 자기상관 계수이다. 시차가 0일 때 자기 상관계수는 항상 1이며 그래프를 확인해 보면 시차가 지날수록 자기 상관 계수가 감소하며 양의 상관관계를 가지는 것을 확인할 수 있다.

2. 이동평균 모델(mr)

ma(moving average)는 자기 자신을 종속 변수로 과거의 오차를 독립변수로 가지는 모델이다. 모델의 현재 값이 이전 시점의 오차들의 선형 조합으로 구성된다는 것을 의미한다.

from statsmodels.tsa.arima.model import ARIMA

np.random.seed(0)
n = 100
ma_params = [0.4,-0.2]
residuals = np.random.normal(0,1,n)

data = [0,0]
for i in range(2,n):
    data.append(ma_params[0] * residuals[i-1] + ma_params[1] *residuals[i-2]+residuals[i])
    
    
    
df = pd.DataFrame({'value': data})

ma 모델을 위해 이동평균계수를 설정하고 정규화된 잔차를 생성한다. 첫번째 이동평균계수에 이전 값의 잔차를 곱한 값에 두 번째 이동평균계수에 두 번째 이전 값을 곱한 값을 더하고 현재 잔차를 더해서 시계열 데이터를 생성한다.

이동평균계수가 2개이므로 이전2개의 잔차가 현재의 데이터에 영향을 주며 ma(2)로 표현할 수 있다.

model = ARIMA(df['value'],order =(0,0,2))
result = model.fit()

print(result.summary())

plt.plot(result.resid)
plt.xlabel('time')
plt.ylabel('residuals')
plt.show()

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                  value   No. Observations:                  100
Model:                 ARIMA(0, 0, 2)   Log Likelihood                -140.502
Date:                Sun, 04 Jun 2023   AIC                            289.003
Time:                        13:14:48   BIC                            299.424
Sample:                             0   HQIC                           293.221
                                - 100                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0436      0.134      0.324      0.746      -0.220       0.307
ma.L1          0.4539      0.093      4.905      0.000       0.273       0.635
ma.L2         -0.0975      0.112     -0.870      0.384      -0.317       0.122
sigma2         0.9695      0.151      6.408      0.000       0.673       1.266
===================================================================================
Ljung-Box (L1) (Q):                   0.00   Jarque-Bera (JB):                 0.28
Prob(Q):                              0.98   Prob(JB):                         0.87
Heteroskedasticity (H):               0.71   Skew:                             0.02
Prob(H) (two-sided):                  0.32   Kurtosis:                         2.75

const 계수는 0.0436이며 유의미하지 않다. ma.l1과 ma.l2는 각각 0.4539, -0.0975이고 ma.l1은 유의미하며 ma.l2는 유의미하지 않은 것을 알 수 있다. sigma2는 잔차의 분산을 나타내며 0.9695이다.

 

ljung-box는 잔차의 자기상관성을 평가하며 l1이 0으로 첫번째 자기 상관계수에 대한 통계량이 0이고 잔차 사이에 자기상관성이 없음을 의미한다. jarque-bera는 잔차의 정규성을 평가하며 0.28이고 p-value인 prob가 0.87으로 정규성을 따른다고 할 수 있다. heteroskedasticity는 잔차의 이분산성이며 0.71이고 p-value가 0.32로 이분산성이 있다고 판단한다.

 

skew는 잔차의 비대칭성을 나타내며 0.02로 거의 대칭이다. kurtosis는 잔차의 첨도를 나타내며  2.75이고 3에 가까울수록 정규분포에 가깝다고 판단한다.

 

summary를 확인하면 잔차간의 자기 상관이 없으며 정규성을 따르고 이분산성성이 존재하는 잔차의 데이터라고 판단할 수 있다.

 

3. arma 모델

arma 모델은 자기회귀 모델과 이동평균 모델의 결합으로 시계열의 자기상관성과 이동평균성을 고려한 모델이며 이전 시전의 값과 오차의 선형 조합이 현재 값을 구성한다는 것을 의미한다.

import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA

np.random.seed(0)
n=100
ar_params = [0.7]
ma_params = [0.4,-0.2]
residuals = np.random.normal(0,1,n)

data = [0,0]
for i in range(2,n):
    ar_term = ar_params[0] * data[i-1]
    ma_term = ma_params[0] * residuals[i-1] + ma_params[1] * residuals[i-2]
    data.append(ar_term + ma_term + residuals[i])
    
df = pd.DataFrame({'Value': data})

ar 계수와 ma 계수를 각각 지정하여=고 데이터를 100개 생성한다. for문으로 2부터 100번까지 돌리고 ar계수에  전의 데이데이터를 곱한 값, ma계수에 전의 잔차를 곱하고 또 다른 ma 계수에 그전 잔차를 곱한 값, 현재시점의 잔차를 모두 더하여 데이터를 생성하고 데이터 프레임으로 저장한다. 

model = ARIMA(df['Value'], order=(1,0,2))
results = model.fit()

print(results.summary())

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                  Value   No. Observations:                  100
Model:                 ARIMA(1, 0, 2)   Log Likelihood                -140.937
Date:                Mon, 05 Jun 2023   AIC                            291.874
Time:                        10:00:50   BIC                            304.900
Sample:                             0   HQIC                           297.146
                                - 100                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.1564      0.510      0.307      0.759      -0.842       1.155
ar.L1          0.7647      0.129      5.934      0.000       0.512       1.017
ma.L1          0.3757      0.158      2.382      0.017       0.067       0.685
ma.L2         -0.1727      0.175     -0.986      0.324      -0.516       0.171
sigma2         0.9663      0.151      6.394      0.000       0.670       1.263
===================================================================================
Ljung-Box (L1) (Q):                   0.01   Jarque-Bera (JB):                 0.19
Prob(Q):                              0.92   Prob(JB):                         0.91
Heteroskedasticity (H):               0.70   Skew:                             0.03
Prob(H) (two-sided):                  0.31   Kurtosis:                         2.80

arima 모델을 사용하여 학습하며 차수를 (1,0,2)로 지정하여 i의 계수를 0으로 설정하고 모델을 학습한다. summary를 확인한다.

plt.plot(results.resid)
plt.xlabel('time')
plt.ylabel('residuals')
plt.show()

resid 함수로 잔차의 패턴을 확인할 수 있다.

pred = results.predict(start=1,end=n)
plt.plot(df['Value'], label='actual')
plt.plot(pred,label='arima')
plt.xlabel('time')
plt.ylabel('value')
plt.legend()
plt.show()

 

모델을 가지고 값을 예측하여 비교한다.

4. arima 모델

arima 모델은 자기회귀 모델과 이동평균 모델을 포함하는 것은 동일하나 차분 개념을 포함하고 있다. arima 모델은 차분 개념을 포함하기 때문에 정상성을 가진 데이터에 적합하다.

정상성이란 시간에 따라 데이터의 특성이 일정하게 유지되는 것이다. 정상성을 가정하면 데이터의 특성이 시간에 따라 변화하지 않기 때문에 분석이나 예측에서 신뢰할 수 있다.

arima 모델을 적용하기 위해서 차분 과정을 통해 정상성을 확보한 후 적용할 수 있다. arima 모델에서 i는 누적(intergrated)를 의미하며 비정상 시계열을 정상 시계열로 변환하기 위해 필요한 차분의 횟수를 의미한다.

model = ARIMA(data, order=(2,1,2))
results = model.fit()
print(results.summary())

pred = results.predict(start='1950-01-01',end='1961-12-01')
plt.plot(data,label='actual')
plt.plot(pred, label='arima')
plt.xlabel('year')
plt.ylabel('passenger count')
plt.legend()
plt.show()

                               SARIMAX Results                                
==============================================================================
Dep. Variable:             Passengers   No. Observations:                  144
Model:                 ARIMA(2, 1, 2)   Log Likelihood                -671.673
Date:                Mon, 05 Jun 2023   AIC                           1353.347
Time:                        12:15:21   BIC                           1368.161
Sample:                    01-01-1949   HQIC                          1359.366
                         - 12-01-1960                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1          1.6850      0.020     83.059      0.000       1.645       1.725
ar.L2         -0.9548      0.017    -55.419      0.000      -0.989      -0.921
ma.L1         -1.8432      0.125    -14.792      0.000      -2.087      -1.599
ma.L2          0.9953      0.135      7.372      0.000       0.731       1.260
sigma2       665.9562    114.130      5.835      0.000     442.266     889.646
===================================================================================
Ljung-Box (L1) (Q):                   0.30   Jarque-Bera (JB):                 1.84
Prob(Q):                              0.59   Prob(JB):                         0.40
Heteroskedasticity (H):               7.38   Skew:                             0.27
Prob(H) (two-sided):                  0.00   Kurtosis:                         3.14

arima 모델을 학습하고 예측한다. summary와 그래프를 그려 실제값과 비교하며 확인한다.

5.sarima 모델

sarima 모델은 arima 모델에 계절성분 s(seasonal)을 추가한 값이다. 계절성이 있는 데이터에 대비할 수 있으며 계절성 자기회귀, 계절성 차분, 계절성 이동평균, 계절성 주기를 추가적인 매개변수로 가진다.

from statsmodels.tsa.statespace.sarimax import SARIMAX

np.random.seed(0)
n =100
data = np.random.normal(0,1,n)
dates = pd.date_range(start='2022-01-01', periods=n,freq='M')

df = pd.DataFrame({'Value':data}, index=dates)

plt.plot(df)
plt.xlabel('date')
plt.ylabel('value')
plt.show()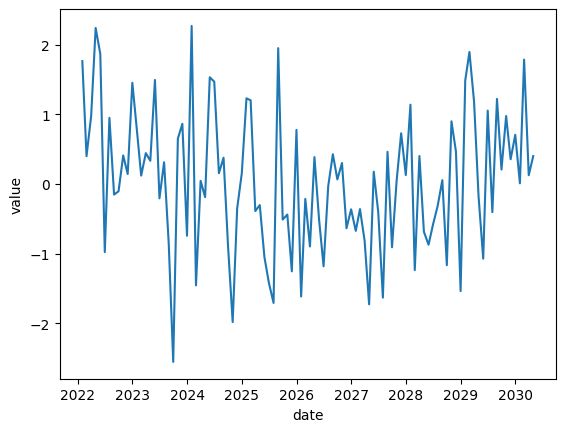

랜던 시계열 데이터를 생성하고 데이터프레임으로 만들어 그래프를 확인한다.

model = SARIMAX(df, order=(1,1,1), seasonal_order=(1,1,1,12))
results = model.fit()
print(results.summary())

                                     SARIMAX Results                                      
==========================================================================================
Dep. Variable:                              Value   No. Observations:                  100
Model:             SARIMAX(1, 1, 1)x(1, 1, 1, 12)   Log Likelihood                -134.870
Date:                            Mon, 05 Jun 2023   AIC                            279.739
Time:                                    12:15:22   BIC                            292.069
Sample:                                01-31-2022   HQIC                           284.704
                                     - 04-30-2030                                         
Covariance Type:                              opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1         -0.0495      0.132     -0.376      0.707      -0.308       0.209
ma.L1         -0.8976      0.074    -12.182      0.000      -1.042      -0.753
ar.S.L12       0.1175      0.230      0.511      0.609      -0.333       0.568
ma.S.L12      -0.7666      0.324     -2.365      0.018      -1.402      -0.131
sigma2         1.1522      0.241      4.773      0.000       0.679       1.625
===================================================================================
Ljung-Box (L1) (Q):                   0.15   Jarque-Bera (JB):                 0.20
Prob(Q):                              0.70   Prob(JB):                         0.90
Heteroskedasticity (H):               0.71   Skew:                            -0.12
Prob(H) (two-sided):                  0.36   Kurtosis:                         3.03

7개의 매개변수를 넣고 sarimax함수로 학습한다. summary로 모델을 확인한다.

pred = results.predict(start='2022-01-31',end='2030-04-30')
plt.plot(df,label='actual')
plt.plot(pred, label='sarima')
plt.xlabel('year')
plt.ylabel('value')
plt.legend()
plt.show()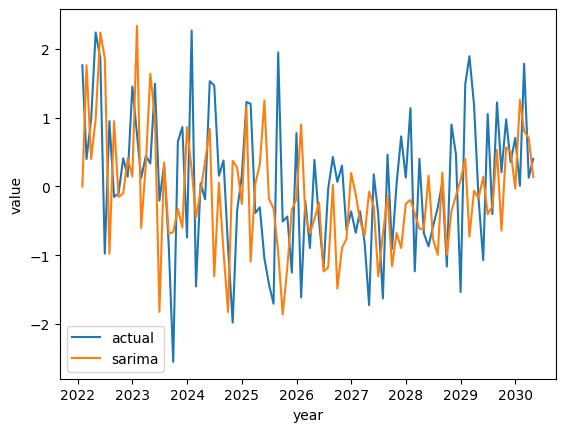

모델을 사용해 값을 예측하고 실제값과 비교한다.

6. aic(Akaike Information Criterion),bic(Bayesian Information Criterion)

aic와 bic는 모델링이 끝난 후 여러 모델링 선택지 중 가장 좋은 모델을 선택하기 위한 방법이다.

aic와 bic는 likelihood(L)가 커질수록, 변수 개수(p)가 작아질수록 작은 값을 가지며 결과 값이 작을수록 모델이 데이터에 잘 적합되고 복잡화를 최소화하는 모델이다. likelihood는 가능도(우도)이며 모델의 적합도이다.

aic는 변수의 개수에 따른 페널티가 일정하지만 bic logn을 곱하기 때문에 더 높은 페널티를 부과한다는 점에서 차이가 있다.

best_aic = np.inf
best_order = None

for p in range(3):
    for d in range(2):
        for q in range(3):
            order = (p,d,q)
            try:
                model = ARIMA(data, order = order)
                results = model.fit()
                aic = results.aic
                if aic <best_aic:
                    best_aic = aic
                    best_order = order
            except:
                continue

print('best aic:', best_aic)
print('best order:', best_order)

best aic: 286.49379665460486
best order: (1, 1, 2)

3개의 루프를 걸어 (0~2,0~1,0~2)의 arima 모델을 탐색하며 현재의 aic 값과 계속하여 비교하여 aic가 가장 낮은 값을 찾는다. (1,1,2)에서 가장 작은 286을 얻을 수 있다.

best_bic = np.inf
best_order = None

for p in range(3):
    for d in range(2):
        for q in range(3):
            order = (p,d,q)
            try:
                model = ARIMA(data, order = order)
                results = model.fit()
                bic = results.bic
                if bic <best_bic:
                    best_bic = bic
                    best_order = order
            except:
                continue

print('best bic:', best_bic)
print('best order:', best_order)

best bic: 296.87427605514324
best order: (1, 1, 2)

bic도 동일하게 루프를 걸어 탐색하며 (1,1,2) 차수에서 296의 값을 얻을 수 있다.

7. 정상성(adf) 감정

adf 감정은 시계열 데이터의 정상성을 평가하는 것이다.

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller

data = pd.read_csv('../data/airline-passengers.csv')
data['Month'] = pd.to_datetime(data['Month'])
data.set_index('Month',inplace=True)

aiplane 데이터를 불러오고 index를 month로 설정한다.

fig, (ax1, ax2) = plt.subplots(2,1,figsize=(8,8))
plot_acf(data, ax=ax1)
plot_pacf(data, ax=ax2)
plt.show()

acf 그래프와 pacf 그래프를 그려 자기상관계수와 부분 자기 상관계수를 확인한다.

result = adfuller(data['Passengers'])
print('adf statistic:' , result[0])
print('p-value:', result[1])
print('critical values:')

for key, value in result[4].items():
    print(f'{key}: {value}')
    
adf statistic: 0.8153688792060441
p-value: 0.9918802434376409
critical values:
1%: -3.4816817173418295
5%: -2.8840418343195267
10%: -2.578770059171598

adfuller 함수를 사용하여 정상성을 평가한다. 통계량 값과 p-value, 임계값들을 확인한다. p-value가 0.05보다 크기 때문에 이 데이터는 정상성을 가지지 않는다고 판단할 수 있다. 어떤 임계값을 선택하더라도 임계값보다 통계량이 크므로 귀무가설을 기각할 수 없다.

8. 잔차 분석

잔차 분석은 모델이 얼마나 데이터에 적합한지 평가하기 위해 사용되며 모델의 예측값과 관측값의 차이이다. 잔차가 정규분포를 따르는지 확인하며 잔차가 자기 상관이 없는지 확인하고 잔차의 분산이 독립변수나 예측 값과 관계없이 일정한지 확인한다.